[캐글필사2-(1)] 타이타닉 EDA 및 Feature Engineering (진행중)

< 필요한 라이브러리 불러오기 > 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_theme(style = 'white', context = 'notebook', palette = 'deep')  
from collections import Counter  

from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

# sns.set :: 그래프 전체적인 스타일을 조절할 수 있다. 

 

 

< 데이터 불러오기 >

train = pd.read_csv('C:/Users/82108/Desktop/kaggle/train.csv')
test = pd.read_csv('C:/Users/82108/Desktop/kaggle/test.csv')
IDtest = test['PassengerId']
train.head()

 

< 이상치 검정 >

# 이상치는 극단적인 영향력을 가지고 있기 때문에 (특히 회귀문제에서), 분석 전에 이상치를 탐색하는 과정이 필요하가.

# 여기서는 Turkey method를 사용하였다 >> boxplot 에서 이상치 나오는 과정을 함수로 만들기

def detect_outliers(df,n,features):
    
    outlier_indices = []  
    
    for col in features: 
        Q1 = np.percentile(df[col],25)
        Q3 = np.percentile(df[col],75)
        IQR = Q3 - Q1
        
        outlier_step = 1.5*IQR
               
        outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
             
        outlier_indices.extend(outlier_list_col)
            
    outlier_indices = Counter(outlier_indices)
        
    multiple_outliers = list( k for k, v in outlier_indices.items() if v > n)
        
    return multiple_outliers
    
Outliers_to_drop = detect_outliers(train,2,["Age",'SibSp','Parch','Fare'])

# 이상치 검출해주는 함수 detect_outliers()

# 함수 전체적인 설명 :: 각 컬럼별(수치형) 이상치를 검정해서 2개 이상의 컬럼에서 이상치가 있는 관측값의 index를                                     outlier_indices에 담을 것이다. 

# for문을 통해 각 컬럼별 Q1,Q3을 구해 outlier_step을 구한다.

# 각 컬럼별로 이상치 기준점 이하 혹은 이상인 관측값의 index를 outlier_list_col에 저장한다.

# 각 컬렴별로 구한 index를 extend 함수를 통해 합친다.

** append()와 extent()의 차이점은 append는 마지막에 값을 하나씩 붙이는 것이고,

                                             extend를 두 개 이상을 한번에 다 붙 일 수 있다. 

 

# Counter 함수 :: 요소의 개수를 알려주는 함수

# outlier_indices 에는 요소들이 인덱스들로 구성되어 있으니 Counter 함수를 통해 각각의 인덱스가 몇개 있는지 알려준다.

 

train.loc[Outliers_to_drop]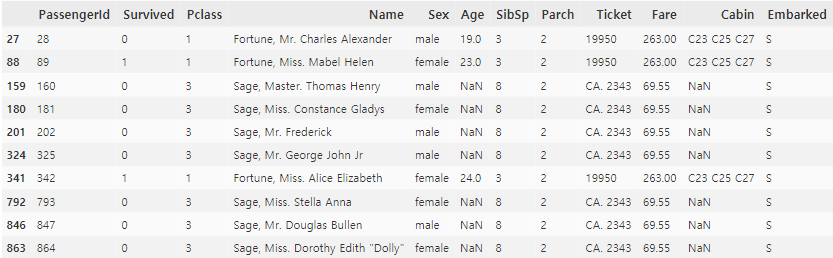

>> 28,89,342 탑승객은 Fare 값이 너무 높고, 나머지 7명은 SisSp가 너무 높다.

 

train = train.drop(Outliers_to_drop, axis = 0).reset_index(drop = True)

# drop() :: row ( axis = 0 )나 columns ( axis = 1 ) 삭제하기 

# dropna() :: 결측치가 있는 행을 모두 삭제할 수 있는 함수 

# drop_duplicates() :: 중복인 행을 삭제할 수 있는 함수 

# reset_index :: 데이터프레임을 먼저 불러온 후, 특정 열을 인덱스로 설정할 때 사용하는 함수 

                  :: drop = True 인덱스로 지정은 하되, 기존열을 남겨놓는다. 

>> 이상치로 추출된 관측값들을 제거하자

 

< train 데이터와 test 데이터 합치기 >

train_len = len(train)
train_len

dataset = pd.concat(objs = [train,test], axis = 0).reset_index(drop = True)
dataset.head()

# Feature Engineering을 같이 해주기 위해 train data와 test data 합친다.

# Categorical conversion 하는 과정에서 같은 수의 features을 얻기 위해서

# 예를 들어, train에는 Age변수에 10대 / 20대 / 30대 의 값이 있고, test에는 10~40대 까지 있다면 

   train으로만 Categorical conversion을 했다면 test에 똑같이 적용하는 과정에서 오류가 발생할 것이다. 

 

< 결측치 확인하기 > 

dataset = dataset.fillna(np.nan)
dataset.isnull().sum() 

# train / test 합친 데이터 dataset 의 결측치 

# 각 컬럼별 분석 시 채울거임

 

 

 

< Feature analysis >

1. Numerical value

g = sns.heatmap(train[['Survived','SibSp','Parch','Age','Fare']].corr(), annot = True , fmt = ".2f", cmap = 'coolwarm')

>> Fare가 Survived와 상관계수가 가장 높으며 유의해보인다. (0.26)

>> 그렇다고 해서 다른 변수들이 쓸모없다는 것은 절대 아니다

 

1-1. SibSp vs Survived

g = sns.factorplot(x = 'SibSp', y='Survived' , data = train, kind = 'bar',
                  size = 6 , palette = 'muted')
g.despine(left = True) 
g = g.set_ylabels("survival probability")

# despine() :: 그래프를 좀 더 깔끔하게 그려주도록 도와주는 함수 

                :: left = True 해줌으로써 왼쪽 축이 없어짐 

>> SibSp가 1~2명일 때, 생존율이 높은 편이며 그 이상으로 갈수록 생존율이 떨어진다. 

 

1-2. Parch vs Survived

g = sns.factorplot(x = "Parch", y = 'Survived', data = train , kind = 'bar', size = 6, palette = 'muted')
g.despine(left = True)
g = g.set_ylabels("survival probability")

>> SibSp와 비슷한 패턴을 보임 

>> Parch가 1~3명에서 생존율이 높은 편이며, 4 이상의 생존율은 거의 없다.

>> 이를 통해 챙겨야 하는 가족의 수가 많아질수록 생존율이 떨어짐을 짐작할 수 있다. 

 

1-3. Age vs Survived

g = sns.FacetGrid(train, col = 'Survived')
g = g.map(sns.distplot, "Age")

##########################################################

g = sns.kdeplot(train["Age"][(train["Survived"] == 0) & (train["Age"].notnull())], color = 'Red', shade = True)
g = sns.kdeplot(train["Age"][(train["Survived"] == 1) & (train["Age"].notnull())], ax = g , color = 'Blue', shade = True)
g.set_xlabel("Age")
g.set_ylabel("Frequency")
g = g.legend(["Not Survived","Survived"])

(왼쪽) FacetGrid // (오른쪽) kdeplot

# FacetGrid() :: 다중 플롯 그리드를 만들어서 여러가지 쌍 관계를 표현하기 위한 그리드 Class이다. 즉, 도화지에 축을 나누는 것과 같다. 

                  :: FacetGrid(data, row, col, hue)  // map함수를 통해 어떤 그래프 그릴것인지 변수명과 함께 명시 

# kdeplot() :: 데이터의 분포를 확인하는 커널 밀도 추청 플롯 

               :: 히스토그램은 구간을 어떻게 설정하느냐에 따라 결과물이 매우 달라진다 >> 대안 >> 커널밀도함수

>> Age 분포는 마치 정규분포와 비슷한 꼴로 나오며, 생존자와 비생존자의 분포가 비슷해보인다.

>> 하지만 큰 차이점은 어린층의 생존율이 훨씬 높음을 알 수 있다. 

>> 반대로 60~80세의 생존율은 낮은 편이다. 

>> KDE를 보면 어린층에서 그래프가 솟아오른걸 볼 수 있다. 

 

1-4. Fare vs Survived

dataset["Fare"].isnull().sum()   # 1개

dataset['Fare'] = dataset["Fare"].fillna(dataset["Fare"].median)

>> 결측치가 1개밖에 없으니 Fare의 중간값으로 채움 >> 큰 영향 없을 것이다. 

 

g = sns.distplot(dataset["Fare"], color="m", label="Skewness: %.2f"%(dataset["Fare"].skew()))
g = g.legend(loc="best")

에러 나는 거 해결중......