이 글은 고려대학교 김성범 교수님의 유튜브 강의를 참고하여 작성한 내용입니다.
https://youtu.be/xki7zQDf74I [핵심 머신러닝] 의사결정나무모델 1 (모델개요, 예측나무)
https://youtu.be/2Rd4AqmLjfU [핵심 머신러닝 ] 의사결정나무모델 2 (분류나무, Information Gain)
의사결정나무 모델이란?
: 데이터에 내재되어 있는 패턴을 변수의 조합으로 나타내는 예측/분류 모델을 나무의 형태로 만드는 것
: 스무고개 놀이와 비슷한 개념

: 핵심은 데이터를 2개 혹은 그 이상의 부분집합으로 분할
: 데이터가 균일해지도록 분할 >> ★균일에 기준이 회귀와 분류마다 다름★
: 분류는 비슷한 범주를 갖고 있는 관측치들끼리 (분류 균일)
: 회귀는 비슷한 수치를 갖고 있는 관측치들끼리 (회귀 균일)
: 뿌리마디 / 중간마디 / 끝마디로 구성
: 뿌리마디는 나무마다 하나만 존재, 중간마다에는 위 아래 가지가 존재, 끝마디는 더이상 분할이 일어나지 않음

: 초기에 60개의 데이터(n=60)가 기준(Price>=9446)에 따라 초기에 48개와 12개로 나뉘어짐
: 48개의 데이터는 또 다른 기준(Type)에 의해 23개와 25개로 이진분할 진행됨
: 이진 분할이 반복적으로 이뤄짐
: 끝마디에 속하는 관측치들을 모두 합치면 60개 초기 데이터 개수와 동일!! (당연?)
의사결정나무 그림으로 이해

: 검은색과 흰색의 관측치들이 섞여 있는데 5개의 박스들로 인해서
어느 정도 균일하게 나누어짐을 알 수 있다.

: 분류그림(1)~(3)은 표현은 다르지만, 의미는 모두 동일
: 분류그림(1)~(2)를 나무로 표현한 것이 분류그림(3)
: 데이터가 3차원이 넘어가면 분류그림(1)~(2)로 표현하는 데 한계가 있어 분류그림(3)으로 표현
Regression Tree 예측나무 모델
: Y가 수치형 변수인 경우
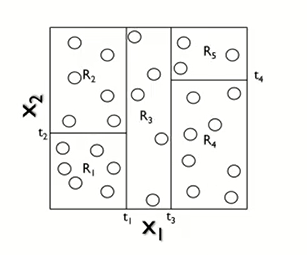
: 변수가 X1,X2 2개이고, 흰 색 동그라미가 관측치 Y이며, Y는 수치형 변수이다.
: 위와 같이 R1~R5 5개의 공간으로 분할했다고 하자. (Train 데이터 학습)

: 그럼 새로운 데이터 (검정 동그라미) 가 왔을 때, 어떻게 예측을 할까?
: 새로운 데이터는 R5에 들어갔으니, R5에 있는 관측값들 1,3,5의 평균인 3으로 예측될 것이다.
(왜 평균으로 예측해? => 이건 뒤에서 자세히~)
: 위의 그림을 나무로 표현하면 아래와 같다.
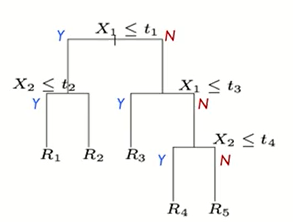

: 예측나무를 함수 형태로 표현할 수 있다.
: I는 지시함수로 :: 중괄호 안이 참이면1, 아니면 0으로 output
: 우리가 고려하는 x1,x2가 Rm이라는 지역에 있니? 있으면 1, 없으면 0 으로 출력
: 만약 새로운 데이터가 R2에 있다면, 나머지 지시함수들은 0이 되며, 결과는 c2만 남을 것이다.
: c2가 새로운 데이터의 예측값이 될 것이다.
: 그럼 c2가 먼데?? 평균일껄?? 왜 ?? 뒤에서 자세한 설명~~

: 1,2,3 번 표현만 다를 뿐, 의미는 모두 같음
Regression Tree 예측나무 모델 - 예제

: 뿌리마디의 392는 전체 표본, 23.45는 392개의 Y의 평균을 의미 (전체 데이터)
: Cylinders가 5보다 작냐 크냐에 따라서 이진 분할 (첫 번째 기준)
: 모든 분할이 끝난 후 각각 끝마디를 보면 392개의 표본이 203/86/103개로 나누어졌다.
: 또한, 각 끝마디의 평균이 29.11/20.23/14.96으로 비슷한 수치들끼리 묶였음을 알 수 있다.
Regression Tree 모델링 프로세스
: 우리가 궁금한건 Cm
: 실제 Y와 예측값 Y_hat 오차제곱의 합을 최소로 하려면 (=비용함수를 최소화 하려면)
각 분할(끝마디)에 속해 있는 y값들의 평균으로 예측했을 때 비용함수가 최소이다.
: 그래서 앞에서 간단한 예제에서도 검은 동그라미를 평균값으로 예측한 것!

Regression Tree - 분할변수&분할점
: 변수가 X1,X2,X3,... 있을 때, 초기 분할 기준을 만약 X1>= 2 일때, 질문!
왜 여기서 초기 기준 변수를 X1으로 했고 왜 그 기준값을 2로 했는가?
즉, 분할변수와 분할점은 어떻게 결정하냐?

: 위의 식 대신 아래의 간단한 예제로 알아보자.

: 위와 같은 데이터가 있을 때,
: 우리가 고려할 것은 6개다 ==> 분할변수3개, 각 분할변수마다 관측치 2개니깐 6개 경우 모두 다해봐!
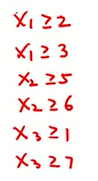
: 6가지 경우 모두 다 했을 때, 비용함수가 가장 작게 나오는 경우 그 때의 분할변수와 분할점을 사용
( 그리드 서치 같은 개념 )
: 쉽게 말해서 모든 경우 다해서 가장 좋은 조합을 분할변수&분할점으로 설정한 거!
Classification Tree 분류 나무 모델
: Y가 범주형 변수인 경우
: 회귀 나무 모델과 거의 유사함

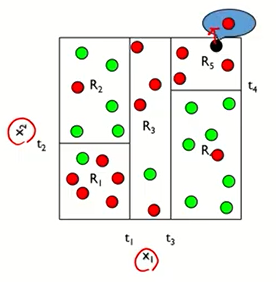
: 빨간색과 초록색의 관측치들이 섞여 있는데 5개의 박스들로 인해서
어느 정도 균일하게 나누어짐을 알 수 있다. (균일~~비슷한 범주끼리)
: 이 때, 검정색의 새로운 관측값이 들어온다면 해당 지역에 빨간색이 대다수(100%)이니 빨간색으로 분류할 것이다.
(회귀에서는 해당 지역의 평균값으로 했지만, 분류에서는 다수결의 원칙으로 분류)

: 클래스 = 범주
: k개의 범주가 있을 때, Rm은 끝노드, Nm은 끝노드에 속하는 관측치 개수를 의미
: Pmk_hat의 의미
= m번째 끝노드에는 Nm개의 관측치들이 있을 것이다.
이 때, Nm개의 관측치는 최대 k개의 범주로 구성되어 있을 것이다.
Pm1 = m번째 끝노드에 1번째 범주의 비율
pm5 = m번째 끝노드에 5번째 범주의 비율
: 새로운 데이터가 끝노드m으로 분류가 되었다면, pmk가 가장 큰 k범주로 분류할 것이다.
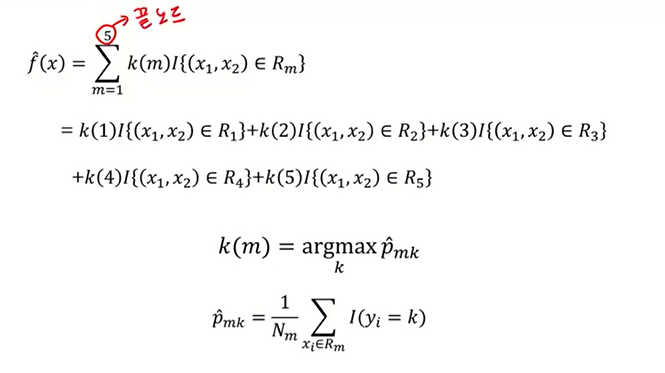
: 분류나무도 함수로 표현할 수 있다. (회귀나무와 거의 동일)
: x1,x2의 패턴을 확인했을 떄, 새로운 데이터가 R3지역으로 분류가 됐다면, k(3)으로 예측할 것이다.
: 그럼 k(3)가 의미하는 것은 머냐? (회귀에서는 평균을 의미했는데 분류에서는?)
: R3에 가장 많은 클래스 비율을 차지하고 있는 k (=k(3))로 output 할것이다.
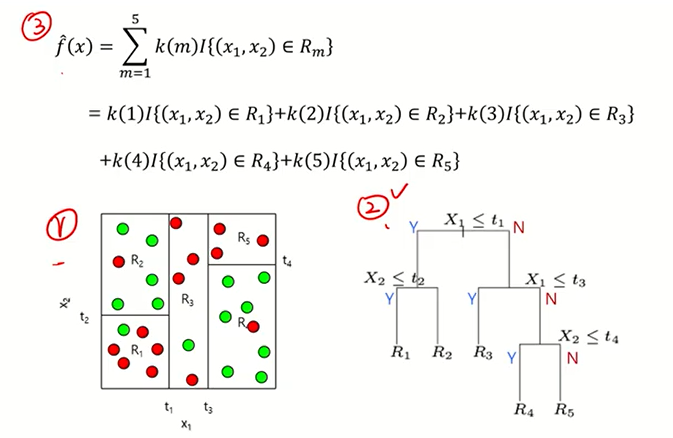
: 1,2,3 형태는 달라도 의미는 똑같다.
: 회귀에서는 y가 수치형 이었기 때문에 오차를 계산할 수 있었지만,
분류에서는 y가 범주이기 때문에 오차를 계산할 수 없다.
: 분류 모델에서는 비용함수가 좀 더 직관적으로 되어 있다.
Classification Tree 분류 나무 모델 - 비용함수
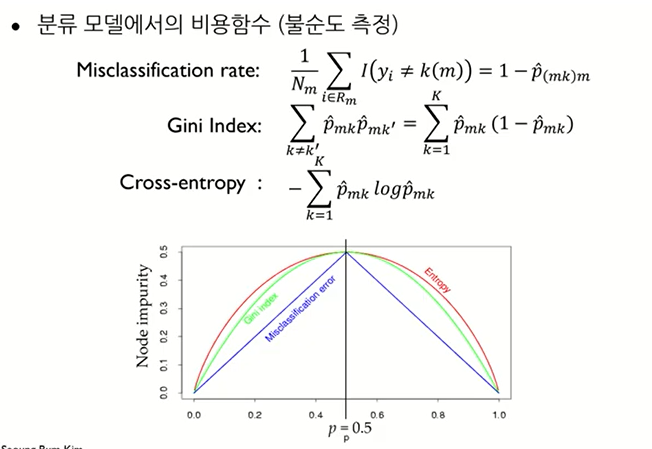
: 분류에서는 비용함수가 3가지가 있다.
: Misclassification rate는 실제와 예측이 얼마나 잘 매칭이 됐는지를 보는 지표이다.
: Gini index / Cross-entropy 는 비율을 통해 나온 값 (pmk활용)
* 이때 *
: Cross-entropy는 p_mk가 1/2이면 1이 된다. 사실 1이 많는데 그래프는 0.5로 되어 있는데 이건 그냥 스케일링 시킨 것
(시각성을 위해)
: 위의 3가지 비용함수 계산은 뒤에서 예제로 직접 계산!
* 각 비용함수에 대한 자세한 설명은 따로 빼서 할 예정 *
Classification Tree - 분할변수&분할점

: 그럼 분류에서는 분할변수와 분할점은 어떻게 결정하나??

: 경우의 수가 무수히 많은데, 다 해봐서 비용함수를 최소화 시키는 j와 s를 결정하는 것

Classification Tree - 분할법칙 & 예시

: 분할법칙은 목표변수가 비슷한 범주끼리 최대한 분할이 될 수 있도록 분할한다.
: 그럼 이 "최대한" 이란 기준은 어떻게 알 수 있을까?
: 순수도 또는 불순도의 측도를 통해서 알 수 있다.
: 각 노드에서 분할변수와 분할점 설정은 불순도의 감소가 최대가 되도록 선택한다.
Classification Tree - 분할변수&분할점. 오분류율

: 초기 데이터가 총 200개 있고, 0범주는 100개, 1범주는 100개 있다.
: 분할 후 왼쪽 노드는 대다수가 0번에 있으니 0번 클래스로 분류할 텐데
21개는 1로 분류했으니 오분류 된 걸로 간주해서 21/84 = 0.25로 오분류율 계산
: 오른쪽 노드는 대다수가 1번에 있으니 1번 클래스로 분류할 텐데
37개는 0으로 분류했으니 오분류 될 걸로 간주해서 37/116 = 0.32로 오분류율 계산
: 총 오분류율은 마지막 식처럼 구합니다.
: L노드와 R노드를 구했으면, 각각의 값에 전체 표본 대비 L,R의 표본 비율을 곱해줍니다.
: 모든 j와 s를 했을 때, 오분류율이 최소화 되는 j와s를 구합니다 (j:분할변수,s:분할점)
Classification Tree - 분할변수&분할점. 지니, 엔트로피

: 얼룩말6마리, 코뿔소1마리 있을 때, 지니계수랑 엔트로피를 구해보자.
: p1=얼룩말일 확률 = 6/7 , p2=코뿔소일 확률 = 1/7 대입해서 지니랑 엔트로피 계산

: 엔트로피 공식은 위의 Entropy(S)와 같다.
: 총 14개의 데이터에서 +는 9개, 5개는 - 라고 했을 때, 엔트로피는 어떻게 계산하나
: + 확률 9/14 , - 확률 5/14 대입해서 계산하면 0.94
정보획득량은 머냐?
: 특정 변수를 사용했을 때 엔트로피 감소량을 의미
: 엔트로피는 무질서도를 의미하는데, 어떤 변수로 인해서 엔트로피가 많이 줄었으면 그 변수는 중요한 것
: 어떤 변수로 인해서 엔트로피 줄었다 = 어떤 변수로 인해 범주가 균일하게 나누어 졌다! = 중요한 변수!
: 특정 변수 A를 사용했을 때, 엔트로피 감소량

: 데이터 설명) Outlook/Temperature/Humidity/Wind 에 따라 Play가 Yes냐 No냐 분류하는 문제
: Wind에 대한 information Gain을 계산해보자
Y를 기준 Yes(+) or No(-)
S는 전체 Y를 의미 => 9+ 5-
=> Entropy(S) 를 구한다.
Sfalse는 Wind 가 False인 경우 중 Y의 분포를 확인한 것 => 6+ 2-
=> Entropy(Sfalse)를 구한다.
=> 전체 데이터 14개 중 false의 비율을 곱해준다.
Strue는 Wind가 True인 경우 중 Y의 분포를 확인한 것 => 3+ 3-
=> Entropy(Strue)를 구한다.
=> 전체 데이터 14개 중 true의 비율을 곱해준다.
전제 엔트로피에서 위의 두개의 값을 빼준값이 Wind의 정보획득량(;Infomation Gain)이다.
: 상대적인 값이니 다른 변수들의 정보획득량과 비교해야 한다.
: 중요한 변수 선택할 때 사용
: 높을 수록 그 변수가 정보를 많이 담고 있다고 해석할 수 있다.
개별 트리 모델의 단점
: 계층적 구조로 인해 중간에 에러가 발생하면 다음 단계로 에러가 계속 전파
: 학습 데이터의 미세한 변동에도 최종 결과 크게 영향
: 적은 개수의 노이즈에도 크게 영향
: 나무의 최종노드 개수를 늘리면 과적합 위험 (Low Bias, High Variance)
: 새로운 데이터의 예측 성능이 떨어짐
: 이를 보완하기 위해 랜덤포레스트 기법이 사용됨
'ML' 카테고리의 다른 글
| Maximal Covering Location Problem(MCLP) 알고리즘 (5) | 2021.09.16 |
|---|---|
| [ISLR] Chapter6. Linear Model Selection and Regularization - Intro (0) | 2021.07.12 |
| [PCA]Principal Components Analysis 주성분분석 - JoJo's Blog (2) | 2021.07.08 |
| [머신러닝&딥러닝] Train / Validation / Test 의 차이 (4) | 2021.02.01 |
| [머신러닝] 군집화(Clustering) (1) | 2020.10.19 |




댓글