" Principal Components Analysis (PCA) "
이 글은 고려대학교 김성범 교수님의 유튜브 강의를 참고하여 작성한 내용입니다.
https://youtu.be/FhQm2Tc8Kic
실제 데이터 분석을 하다보면 변수가 너무 많아서 머부터 시작해야 될지 혹은 이 변수들을 모두 사용해야 할지
고민하다 보면 어느새 하루가 지나가죠... º_º 오늘은 이 고민을 해결해 줄 PCA에 대해 알아보겠습니다.

p=100인 위의 데이터를 분석 해야한다고 가정해보자
초기에는 데이터의 전반적인 분포를 확인해야 하는데, 변수가 너무 많을 때
즉, 고차원의 데이터를 만났을 때 우리가 할 수 있는 방법은 무엇이 있을까?
그전에, 고차원의 데이터는 왜 분석하는데 어려움이 있을까?
첫 번째) 3차원 이상의 데이터를 시각적으로 표현하는데 한계가 있다.
두 번째) 차원이 클수록 계산 복잡도가 높아져서 모델링이 비효율적이다.
위의 이유로 우리는 중요한 변수들로 차원을 줄일 필요가 있다. 이것을 '차원 축소'라고 한다.
'차원 축소'는 2가지 종류로 구분할 수 있다.
첫 번째, 변수 선택 (Featuer Selection)
: 분석 목적에 부합하는 소수의 예측 변수만을 선택하는 것
: 장점) 선택한 변수들의 해석이 용이하다.
=> X1~Xp 중 중요하다고 생각되는 변수를 뽑을 뿐, X 그대로 사용하기 때문에 해석 용이
: 단점) 변수간 상관관계 고려가 어렵다.
=> 다변량 데이터에서는 변수간 상관관계가 존재할 텐데, 이를 고려하기 어렵다.
두 번째, 변수 추출 (Feature Extraction)
: 예측변수의 변환을 통해 새로운 변수 추출
: 장점) 변수간 상관관계 고려, 일반적으로 변수의 개수를 많이 줄일 수 있다.
: 단점) 추출된 변수의 해석이 어렵다.
=> Z = f(X1, X2,..., Xp) 즉, 새로운 변수 Z는 X들의 결합으로 구성되어서 해석이 어렵다.
지도 학습 / 비지도 학습에 따라 변수 선택 / 변수 추출하는 방식에 차이가 있다.
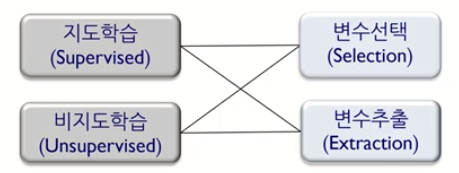
첫 번째, 지도 학습 (Supervised Learning)
1). Supervised feature selection 지도 학습 변수 선택법
: Information gain
: Stepwise regression
: LASSO
: Genetic algorithm
2). Supervised feature extration 지도 학습 변수 추출법
: Partioal least squares; PLS
두 번째, 비지도 학습 (Unsupervised Learning)
1). Unsupervised featuee selection 비지도학습 변수 선택법
: PCA loading
2). Unsupervised feature extration 비지도 학습 변수 추출법
: Principal component analysis ; PCA
: Wavelets transforms
: Auto encoder
" Principal Components Analysis (PCA) "
PCA 개념에 대해 알아보자
: 고차원 데이터를 효과적으로 분석하기 위한 기법 중 하나
: 목적) 차원 축소, 군집화, 시각화, 압축 등
: n개의 관측치와 p개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터로 요약하는 방식
이때, 요약된 변수는 기존 변수의 선형 조합으로 생성된다.
: 원래 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 사영시키는 기법
: 전체 분석 과정 중 주로 초기에 데이터가 어떻게 생겼는지 파악하기 위해 사용된다. (변수 많을 때)
: 핵심 1) 원래 데이터의 정보를 차원을 줄였음에도 불과하고 잘 보존하는 패턴을 보이는 게 핵심!
: 핵심 2) 새로 생성된 Z는 p개의 X들의 선형 결합이다.
즉, p개 중 일부의 선형결합이 아닌 모든 X들에 대한 선형결합이다.
PCA 간단한 표기에 대해 알아보자

: 원래 데이터가 p개의 변수로 구성되었다면, PCA결과 생성된 Z도 p개가 생성된다.
: 이때, Z들을 '주성분'이라고 하며, Z1~Zp는 상관관계가 없다.
: X는 우리에게 주어진 데이터이므로 우리가 구해야 하는 것은 알파!
간단한 예시를 확인해보자
아래의 9개의 관측치가 있다고 할 때,
각각의 축으로 데이터들을 사영시켰을 때, 좌측 기저와 우측 기저 중에서 손실되는 정보의 양(분산의 크기)이 큰 것은 어떤 기저일까?

정답은 좌측 기저이다.
좌측 기저가 우측 기저에 비해 손실되는 정보의 양(분산의 크기)이 적으므로 상대적으로 선호되는 기저라고 할 수 있다.
이제 PCA를 수리적으로 접근해 볼 것이다.
그전에 간단한 수리적 용어들을 살펴보자.
X들의 정보를 요약해주는 3가지를 살펴보자

첫 번째, Mean Vector 평균 벡터
두 번째, Covariance Matrix 공분산 행렬
세 번째, Correlation Matrix 상관관계 행렬
* 공분산의 대각 성분은 각 변수의 분산, 비 대각 성분은 대응하는 두 변수의 공분산을 의미 *
* 공분산과 상관관계의 자세한 개념은 나중에 따로 정리하려고 한다 *
* 데이터의 총분산은 공분산 행렬의 대각 성분들의 합과 같다!
즉, 데이터의 총 분산 = X1의 분산 + X2의 분산 +... + Xp의 분산
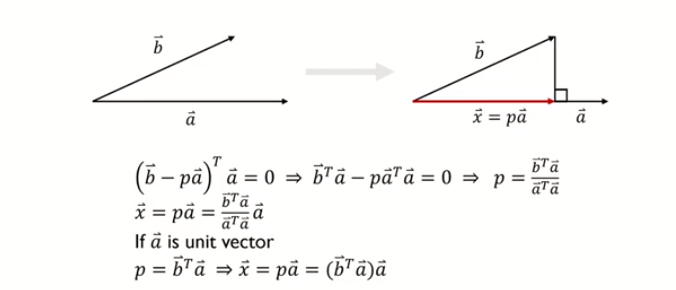
사영(Projection)
: 한 벡터(b)를 다른 벡터(a)에 사영시킨다.
: 벡터(b)로부터 벡터(a)에 수직인 점까지의 길이를 가지며 벡터(a)와 같은 방향을 갖는 벡터를 찾는다는 것을 의미
: 핵심) 같은 방향을 갖는 벡터를 찾는다! (= 방향이 변하지 않는다)
고유값 & 고유벡터 (eigen value & eigen vector)
* 자세한 개념은 나중에 따로 정리하려고 한다 *
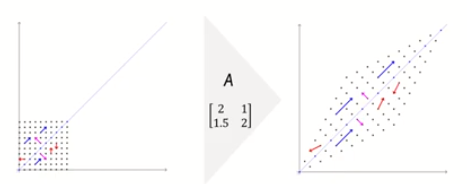
: 어떤 행렬 A에 대해 상수 λ 와 벡터 x가 아래의 식을 만족할 때, λ와 x를 각각 행렬 A의 고유값 / 고유 벡터라고 한다.
Ax = λx => (A-λI) x = 0
: 쉽게 말해, 행렬 A의 고유값 / 고유 벡터는 행렬 A의 대표하는 특징이라고 볼 수 있다.
Ax = λx => (A-λI) x = 0 이 식의 의미를 좀 더 살펴보자.
: 벡터(x)에 행렬(A)을 곱한다는 것은 해당 벡터(x)를 선형 변환한다는 의미이다. = Ax
: 벡터(x)에 상수(λ)를 곱한다는 것은 크기만 변하고 방향은 변하지 않는 벡터를 의미한다 = λx
=> 위의 2가지 해석을 종합하면 고유 벡터(x)는 이 변환에 의해 방향이 변하지 않는 벡터를 의미한다.
PCA 알고리즘에 대해 배우기 전
아래의 4가지를 읽어보자.

: 각 변수들이 평균이 0이 되도록 작업해준다.
: ∑ 는 X의 공분산 행렬 => p by p matrix
: α 는 앞에서 언급했듯이 Z를 생성하기 위해 X들에 곱해지는 상수이다.
: 이때, α 는 모든 값을 가질 수 있는 것은 아니고 크기가 1이라는 제약을 줄 것이다.
: 최종적으로 Z = αTX 형태로 나타낼 수 있다
=> 우리의 목표는? 고차원을 저차원으로 줄이는 것
=> 어떻게? X들의 결합으로 나타낸 Z를 활용할 것
=> Z를 구하기 위해서는? α 를 찾아야 한다!!!!!!!!!!!!!!!
=> α 는 어떻게 찾아? Z의 분산을 최대화시켜주는 α 찾기 (최적화 문제)
즉, PCA 알고리즘의 핵심은 Z의 분산을 최대화시켜주는 α 를 찾는 것이다!!
여기서부터는 직접 필기한 내용으로 설명을 진행하려고 한다.

최종적으로 우리는 Z의 분산을 최대로 시켜주는 α 를 찾았다!
α 는 COV(X)의 고유값을 구했을 때, 가장 큰 고유값에 대한 고유 벡터를 의미한다.
실제 예제를 보면 더 쉽게 이해할 수 있을 것이다.
n = 5 , p = 3 인 데이터가 있다고 해보자
첫 번째 과정은 X1, X2, X3들의 평균이 0이 되도록 조정해주는 것이다.

두 번째 과정은 X들의 공분산 행렬 (혹은 상관관계 행렬)을 구한다.
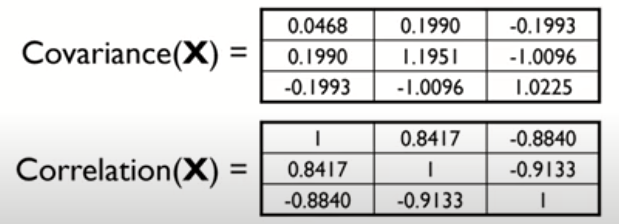
세 번째 과정은 공분산 행렬 (혹은 상관관계 행렬)의 고유값과 고유 벡터를 구한다. (스펙트럼 분해)

위의 1~3 과정을 정리하면 다음과 같다.
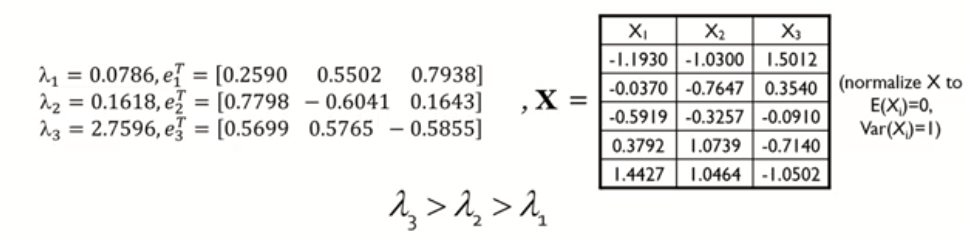
가장 큰 고유값은 λ3이다.
* 이때, X의 변수가 3개이니 (p=3) 주성분 Z도 3개가 나올 것이다 => Z1, Z2, Z3
* [그림 1]에 의해 α = e1이다.
* 즉, Z1 = αTX = e1X

* 그럼 Z2, Z3은 어떻게 구해?
* Z1이랑 같은 방식으로 구하면
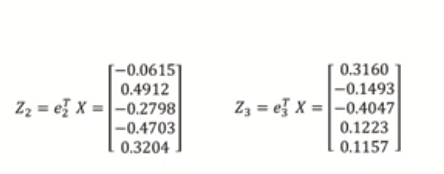
최종적으로 주성분은 다음과 같다.

이렇게 구한 Z 주성분 행렬의 공분산을 구해보면
: 대각 원소는 각각 Z1, Z2, Z3의 분산을 의미한다.
: 그 값을 자세히 보면 위에서 X의 공분산 행렬의 고유값과 동일함을 알 수 있다.
: 비대각원소는 Z끼리의 공분산을 의미하는데 모두 0이다
: 그 말은 Z끼리는 서로 독립임을 의미한다.

자 그럼 X1, X2, X3의 예측 변수들의 결합으로 Z1, Z2, Z3의 주성분을 생성했다.
그럼 몇 개의 주성분을 사용하는 게 좋을까?
Z들의 분산을 통해 몇 개를 분석에 사용할지 결정할 수 있다.

위에서 Z의 공분산 행렬의 대각 원소는 각 Z들의 분산을 의미한다고 했다.
첫 번째 Z1이 전체 데이터 분산 중에서 차지하는 비율을 구해보면
가장 마지막 식으로 표현할 수 있다.
Z1, Z2, Z3의 분산을 의미하는 고유값들의 합을 분모로
Z1의 분산인 λ3을 분자로 했을 때, 0.920의 의미는
Z1만으로 전체 데이터의 92%의 분산(정보)이 보존된다고 해석할 수 있다.
이 값을 Z1, Z2, Z3에 대해서 모두 구한 후 plot을 그려보면 아래와 같다.
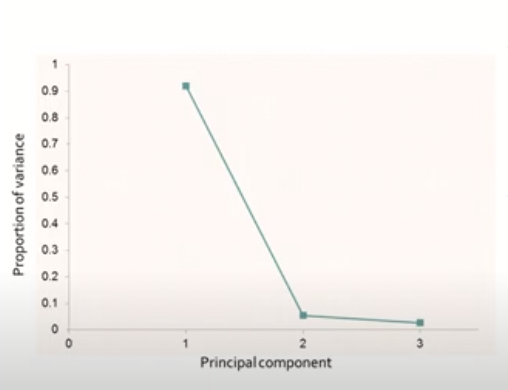
고유값 감소율이 유의미하게 낮아지는 Elbow Point에 해당하는 주성분 수를 선택한다.
여기서는 주성분 1개만으로 데이터의 분산을 거의 보존하고 있다고 볼 수 있다.
만약, Elbow Point로 판단하기 애매하다면,
일정 수준 이상의 분산 비를 보존하는 최소의 주성분을 선택하면 된다
보통 분산 70% 이상을 기준으로 선택
지금까지 PCA과정을 요약하자면

* 이때, 만약 평균을 0으로 센터링하지 않을 거라면 공분산 행렬보다는 상관관계 행렬을 사용하는 게 더 좋다!
'ML' 카테고리의 다른 글
| 의사결정나무(Classification&Regression)-JoJo's Blog (0) | 2021.08.09 |
|---|---|
| [ISLR] Chapter6. Linear Model Selection and Regularization - Intro (0) | 2021.07.12 |
| [머신러닝&딥러닝] Train / Validation / Test 의 차이 (4) | 2021.02.01 |
| [머신러닝] 군집화(Clustering) (1) | 2020.10.19 |
| [ISLR] 8. Tree-Based Methods ( 진행중 ) (0) | 2020.10.13 |




댓글