다음 내용들은 아래의 책 ISLR 책을 해석하면서 공부한 내용임을 먼저 말씀드립니다! ( 사진에 링크 연결 )
Decision tree는 regression과 classification 문제에 적용할 수 있다.
< Decision tree for Regression >

Regression Tree를 설명하기 위해 간단한 예제로 먼저 살펴보겠습니다.
< predicting Baseball Players's Salaries Using Regression Trees >
FIGURE 8.1 를 다시 그려보면
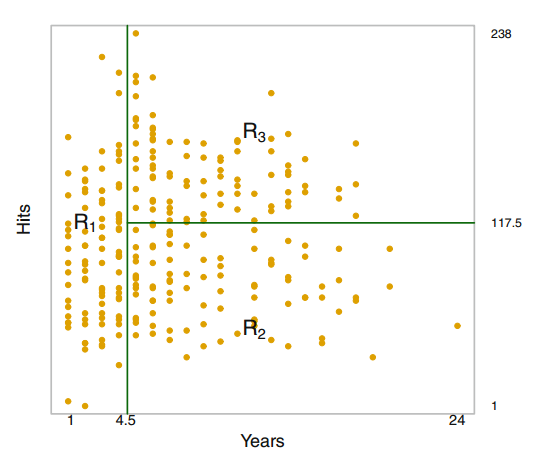
다음과 같이 나타낼 수 있습니다.
첫 번째로는 Years < 4.5를 기준으로 나눌 수 있고,
Years > 4.5로 분류된 데이터들은 다시 한번 Hits < 117.5를 기준으로 분류되었습니다.
" The predicted salary for these players is given by the mean response value for the players in the data set "
예측값은 각 그룹 데이터들의 평균 값 입니다.
즉, R1로 분류된 선수들의 salary평균은 5.107이며, 이 데이터는 log(salary) 데이터이기 때문에
실제 예측 salary 값은 e^5.107 = $165,174입니다.
" terminal node & leaves "
FIGURE8.1에서 가장 밑에 있는 leaf를 terminal node 라고 부릅니다.
"internal node "
FIGURE8.1에서 가지가 나눠지는 부분, Years < 4.5 & Hits < 117.5 가 위치한 곳을 internal node라고 부릅니다.
< Prediction via Stratification of the Feature Space >

예를들어,
Step 1에서 R1 , R2라는 두 개의 region을 얻었다고 하자.
R1의 평균은 10이고, R2의 평균은 20이다.
즉, 새로운 데이터가 들어와서 R1으로 분류되면 그 데이터의 예측값은 10이고, R2로 분류되면 20으로 예측할 것이다.
' 그렇다면 우리는 어떻게 R1,R2,...,Rj로 분류를 할 수 있을까? '
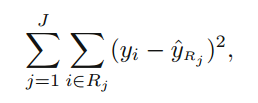
위의 식 RSS를 최소화 시키는 방향으로 R1, R2,..., Rj를 구할 수 있다.
* 이때, yRj hat 은 Rj에 속하는 데이터들의 평균값이다.
하지만 우리는 불행히도 모든 가능한 조합들을 조합시킴으로써 R1,R2,....,Rj들의 조합을 찾기에는 한계가 있다.
그래서 쓰는 방법이
" top - down, greedy approach that is known as recursive binary spliting "
>> each d split is indicated via two new branches further down on the tree
>> the best split is made at that particular step , 과거나 미래의 변화를 보지 않고 바로 앞에 있는 것만 봄
1. 하나의 변수를 선택한다. ( Xj )
2. { X | Xj < s } and { X | Xj > s }에서 RSS를 가장 최소화시키는 s를 찾는다.
3. 1~2과정을 X1~Xp까지 각각 한다.
4. 3과정 나온 p개의 RSS 중 가장 작은 RSS를 가진 Xj와 s조합을 선택한다.
5. 위에서 구한 R1, R2 각각의 regions에서 위의 과정을 반복한다.
6. 우리가 세운 기준에 도달할 때까지 계속 반복하면서 나무를 키운다
* 여기서 기준은 다양한데 예를들면 region에 5개 이하의 관측값이 들어오게 되면 멈춘다 라는 기준 *
1~4 과정을 식으로 표현해보면

< Tree Pruning >
위에서 언급된대로 나무의 크기를 크게 만들게 되면 training set에는 좋은 예측력을 가지는 모델이 만들어질 것이다.
하지만 그것은 Overfit 되었을 것이고 test 데이터에는 형편없는 예측력을 가지게 될 가능성이 높다.
오히려 적은 분할을 가진 작은 트리가 bias는 조금 포기하더라도 더 작은 variance와 더 좋은 해석력을 가질 수 있다.
이를 가능하게 하는 한 가지 대안은 각 분할에 따른 RSS감소가 임계값을 초과하는 경우에만 트리를 구축하는 것이다.
>> 즉, 무조건 RSS가 감소한다고 해서 분할을 하는 것을 방지하기 위해서
이 전략은 더 작은 나무를 만들 수 있게 하고, 쓸모없는 분할들을 없앰으로써 나중에 더 좋은 RSS의 감소로 이어질 수 있다.
즉, 우리의 가장 좋은 전략은
트리를 키울 수 있을 때까지 키운 후 (T0), 그러고 나서 prune과정 (가지치기)을 함으로써 subtree를 얻는 것이다.
" 그렇다면 우리는 어떤 기준으로 prune을 해야 할까? "
직관적으로, 우리의 목표는
" 가장 작은 test error rate를 이끄는 subtree를 찾는 것 "이다.
우리는 subtree를 구했다면, cross-validation 혹은 validation set approach 과정을 통해 test error를 구할 수 있다.
하지만, 모든 가능한 subtree의 cross-validation erorr를 구하는 것은 부담스러운 일이다.
이때, 우리가 사용할 수 있는 방법은 Cost complexity pruning - also known as weakest link pruning
Cost complexity pruning - also known as weakest link pruning
> We consider a sequence of trees indexed by a nonnegative tunning parameter (알파)

1. 반복적인 이 분할을 통해 training data로 학습한 커다란 트리를 만든다.
( 언제까지? terminal node에 최소 관측값이 남아있을 때까지 / 다른 경우도 설정 가능 )
2. cost complexity pruning을 사용해서 최고의 subtrees를 찾는다.
3. 이때, 적절한 알파를 찾기 위해 K-fold cross - validation을 사용한다.
training data를 K개의 folds로 나눈 후,
(a). 위의 1~2 과정을 반복한다.
(b). 남은 kth fold 데이터로 MSE를 구한다.
(c). 각각의 알파에 대해서 나온 k개의 MSE의 값을 평균을 낸다.
(d). (c)에서 나온 MSE값들 중 가장 작은 MSE를 가지는 알파를 찾는다.
4. 찾은 알파를 통해 2단계를 시행하여 subtree를 찾는다.
알파가 0이면 ---> T는 T0와 같아질 것이다. 가지치기의 의미가 전혀 없어진다.
알파가 커지면 --> terminal nodes가 많아지면 지불해야 할 대가가 많아진다. 따라서 크기를 최소화하려고 할 것이다.
** 마치, 라쏘에 정규화 식이랑 비슷한 느낌 **
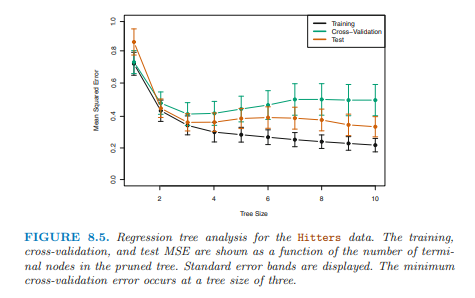
Tree Size가 커짐에 따라 Training data의 MSE는 감소하고 있다.
하지만, Test data의 MSE와 CV MSE는 Tree Size가 3일 때 가장 작은 것을 확인할 수 있다.
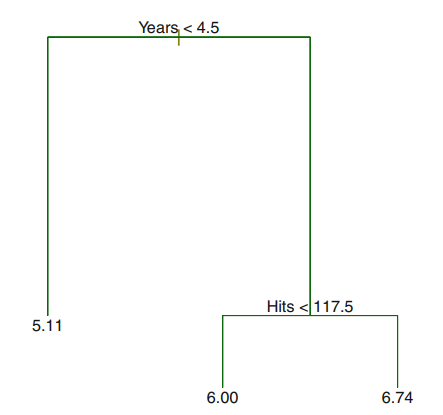
그래서 최종적인 pruned tree는 아래와 같다.
< Decision tree for Classification>
'ML' 카테고리의 다른 글
| 의사결정나무(Classification&Regression)-JoJo's Blog (0) | 2021.08.09 |
|---|---|
| [ISLR] Chapter6. Linear Model Selection and Regularization - Intro (0) | 2021.07.12 |
| [PCA]Principal Components Analysis 주성분분석 - JoJo's Blog (2) | 2021.07.08 |
| [머신러닝&딥러닝] Train / Validation / Test 의 차이 (4) | 2021.02.01 |
| [머신러닝] 군집화(Clustering) (1) | 2020.10.19 |





댓글